Coursera:Nand2Tetris-Note1
Nand2Tetris PartⅠ笔记
目录:
- Boolean Logic 布尔逻辑
- Boolean Functions Synthesis 布尔函数合成
- Logic Gates 逻辑门
- Hardware Description Language硬件描述语言
- Hardware Simulation 硬件模拟
- Multi-Bit Buses 多位总线
- Project 1 (Q&A) 项目Ⅰ
Boolean Logic 布尔逻辑
首先基础的介绍一些布尔逻辑里面的计算/语法
1.(x AND y)
| x | y | AND |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
2.(x OR y)
| x | y | OR |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
3. NOT(x)
| x | NOT |
|---|---|
| 0 | 1 |
| 1 | 0 |
我想这些都很容易理解 其中的0/1也可以叫做”是/否”或者”正/负”。 这具体怎么规定没有所谓 反正象征着有且仅有的两种独立的状态。
其中AND/OR/NOT都为输出结果 左侧为输入的状态。由此我们掌握了最简单的Boolean Logic的基本算式 随之我们也发现这些语法和数学计算的相似之处。
计算部分讲解
优先计算:
- e.g. NOT(0 OR (1 AND 1))=NOT(0 OR 1)=NOT(1)=0
贝尔逻辑也是根据括号里面来确定优先级
真值表与布尔函数对应: - 我们设一个Boolean Function为
f(x,y,z)=(x AND y) OR (Not(x) AND z)
然后我们就能通过枚举不同情况得到一个表格 就像上方的AND/OR/NOT语法一样:
| x | y | z | f |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 |
在Boolean Logic的概念里 这个表格和上面的f(x,y,z)所传达出来的信息是完全一样的 它的正式名字叫真值表。布尔函数和它的真值表这两者本身在意义上是等价的。
Commutative Laws 交换律
- (x AND y)=(y AND x)
(x OR y)=(y OR x)
Associative Laws 结合律
- (x AND (y AND z))=((x AND y) AND z)
(x OR (y OR z))=((x OR y) OR z)
Descriptive Laws 分配律
- (x AND (y OR z))=(x AND y) OR (x AND z)
(x OR (y AND z))=(x OR y) AND (x OR z)
De Morgan Laws
这个定律有别于上面可以类比数学的定律 它是由于Boolean Logic本身的性质而产生的
- NOT (x AND y)=NOT(x) OR NOT(y)
NOT (x OR y)=NOT(x) AND NOT(y)
掌握了这四条公式 我们就可以对几乎所有的复合Boolean Function来进行简化/变形 下面是一个例子:
NOT(NOT(x) AND NOT(x OR y))
=NOT(NOT(x) AND (NOT(x) AND NOT(y)))
=NOT((NOT(x) AND NOT(x)) AND NOT(y))
=NOT(NOT(x) AND NOT(y))
=NOT(NOT(x)) OR NOT(NOT(y))
=x OR y
或者呢 运用上面的结论:真值表与函数对应。当输入00/01/10/11所有的四种组合后 看对应的数值表我们也能得出这个式子到底化简后代表什么 这在逻辑处理上很有意义。
Boolean Functions Synthesis 布尔函数合成
上面讨论了什么是布尔函数/布尔值/布尔代数和相关的性质公式。现在做的是讨论如何从更原始的运算中构造布尔函数。
比如我们这里给出一个布尔函数f(x,y,z)
| x | y | z | f |
|---|---|---|---|
| 0 | 0 | 0 | 1 |
| 0 | 0 | 1 | 0 |
| 0 | 1 | 0 | 1 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 0 | 1 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 0 |
| 1 | 1 | 1 | 0 |
对每一行做出”对应”的“附属”布尔函数。比如第一行的输入是(0,0,0)输出是1 我们构造一个新的布尔函数附属于这一行。即除了输入(0,0,0)输出是1 剩下的情况全输出0。
在第一行的要求下得到式子 (NOT(x) AND NOT(y) AND NOT(z))
当然 很相似的我们对f(x,y,z)里输出为1的每一行都可以创造出这样的”附属函数” 我们就可以用OR来连接他们每一行 然后只用布尔运算符来描述函数f了。
类比上例 我们为3/5行分别做出”附属“函数
得到(NOT(x) AND y AND NOT(z))和(x AND NOT(y) AND NOT(z))
这样我们把这些式子整个用OR链接得到
(NOT(x) AND NOT(y) AND NOT(z)) OR (NOT(x) AND y AND NOT(z)) OR (x AND NOT(y) AND NOT(z))
是的 这个组合起来的函数意味着仅在(0,0,0)/(0,1,0)/(1,0,0)上输出1 其余为0 正是f(x,y,z)。
当然 有趣的是它完全可以利用讲过的性质公式大幅化简
得到 NOT(z) AND (NOT(x) OR NOT(y))
它们或许看起来复杂程度上差距很大 但在逻辑上它们完全等价。
显然我们已经证明了一个非常伟大的或者说非常重要的结论。
无论多么复杂的布尔函数 我们都能仅通过AND/NOT/OR来表达出它们
有人就会问:主播主播 虽然你用三种运算就能表示所有函数 但是有没有更强势的运算符
有的有的 兄弟 有的有的 比NOT/AND还强势的NAND函数来了
| x | y | NAND |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
通过转换得到
(x NAND y ) = NOT(x AND y)
NOT(x) = (x NAND x)
(x AND y) = NOT(x NAND y) = ((x NAND y) NAND (x NAND y))
不难发现 使用NAND函数我们就已经可以完全替代NOT与AND函数 进一步减少了需要用到的运算符种类。
当然了 我们马上就会发现事实中的运算门还会有更多 输入的(x,y)有四种组合对应四个输出结果 按照结果的0/1组合 运算符的种类也应该更多。在下面我们会更详细的讲解这些”运算符”。
Logic Gates 逻辑门
上面的所谓”运算符” 正式名称叫做逻辑门。
现在要给出逻辑门的进一步定义。粗略地说 它是一种使用逻辑门实现布尔函数的技术。逻辑门是一种独立的芯片 旨在提供明确定义的功能的基本芯片。
Elementary: 简单结构 如NAND/NOT/OR/AND/…
Composite: 复合结构 如Mux/Adder/…
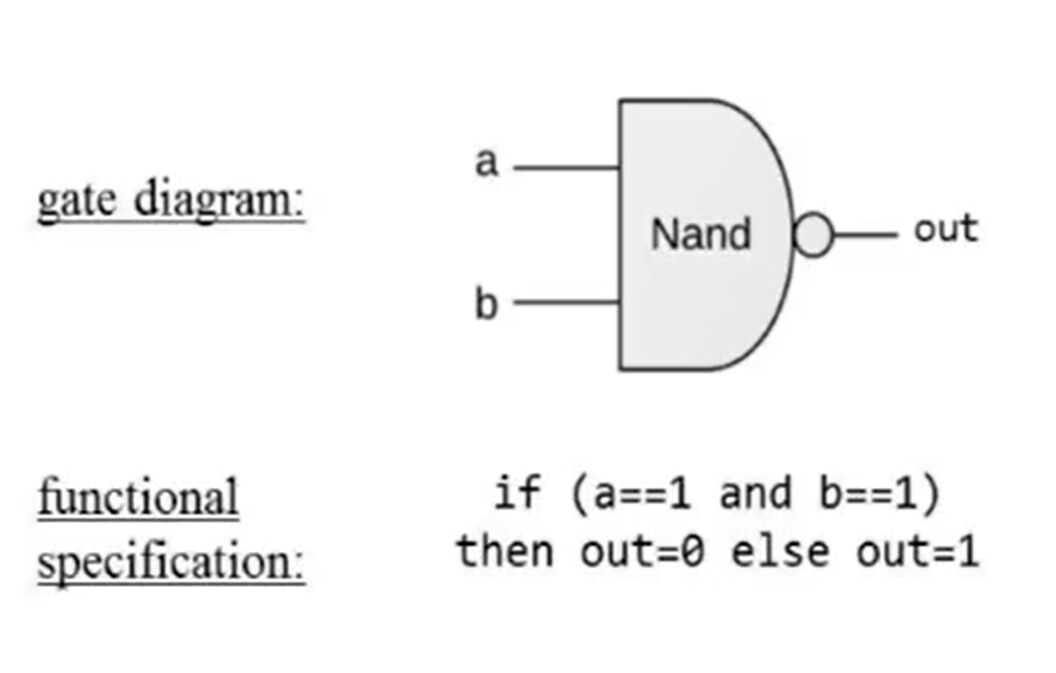
这些逻辑门的输入输入对应关系并不难理解 事实上用电路的模拟我们也能做到描述逻辑门
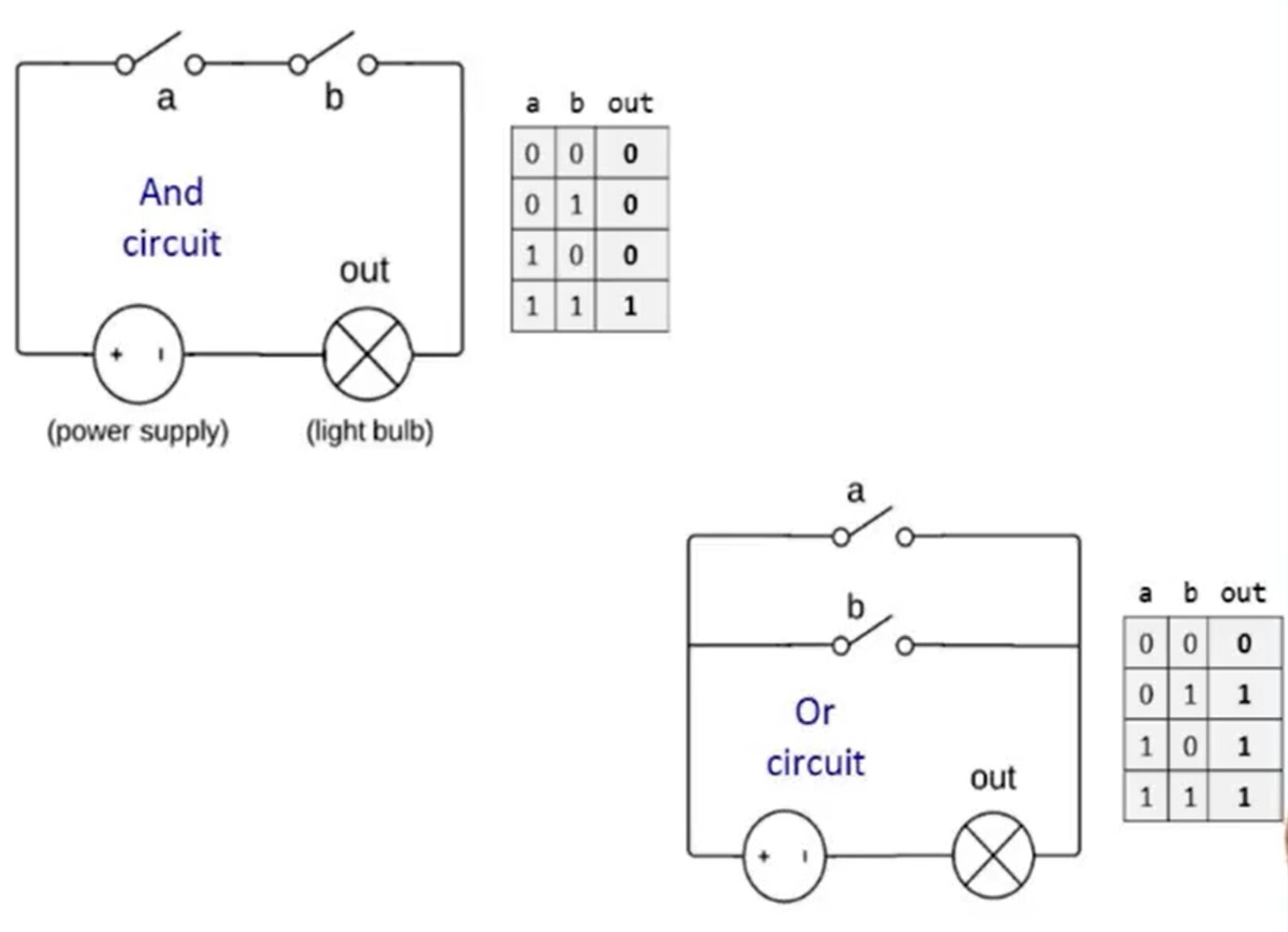
这门课程中 我们不涉及物理实现 一切都在硬件模拟器上进行。无关诸如电路/晶体管/继电器 那些在逻辑门的使用上我们归入计算机科学。而所有依托芯片电路的”实现”均是电气工程。那些使用电路和类似技术建造这些Logic Gate的人被称为电气工程师 而非码农什么的。
当然了 关于逻辑门的种类许许多多 下面介绍一些 后面的project中我们会多多再见的
- NOT 非门
- AND 与门
- NAND 与非门
- NOR 或非门
- XOR 异或门
- XNOR 同或门
- Inverter 逆变器
- Buffer 缓存
Hardware Description Language硬件描述语言
在Nand2Tetris里我们使用名为硬件描述语言或HDL的形式来实际构建和实现逻辑门。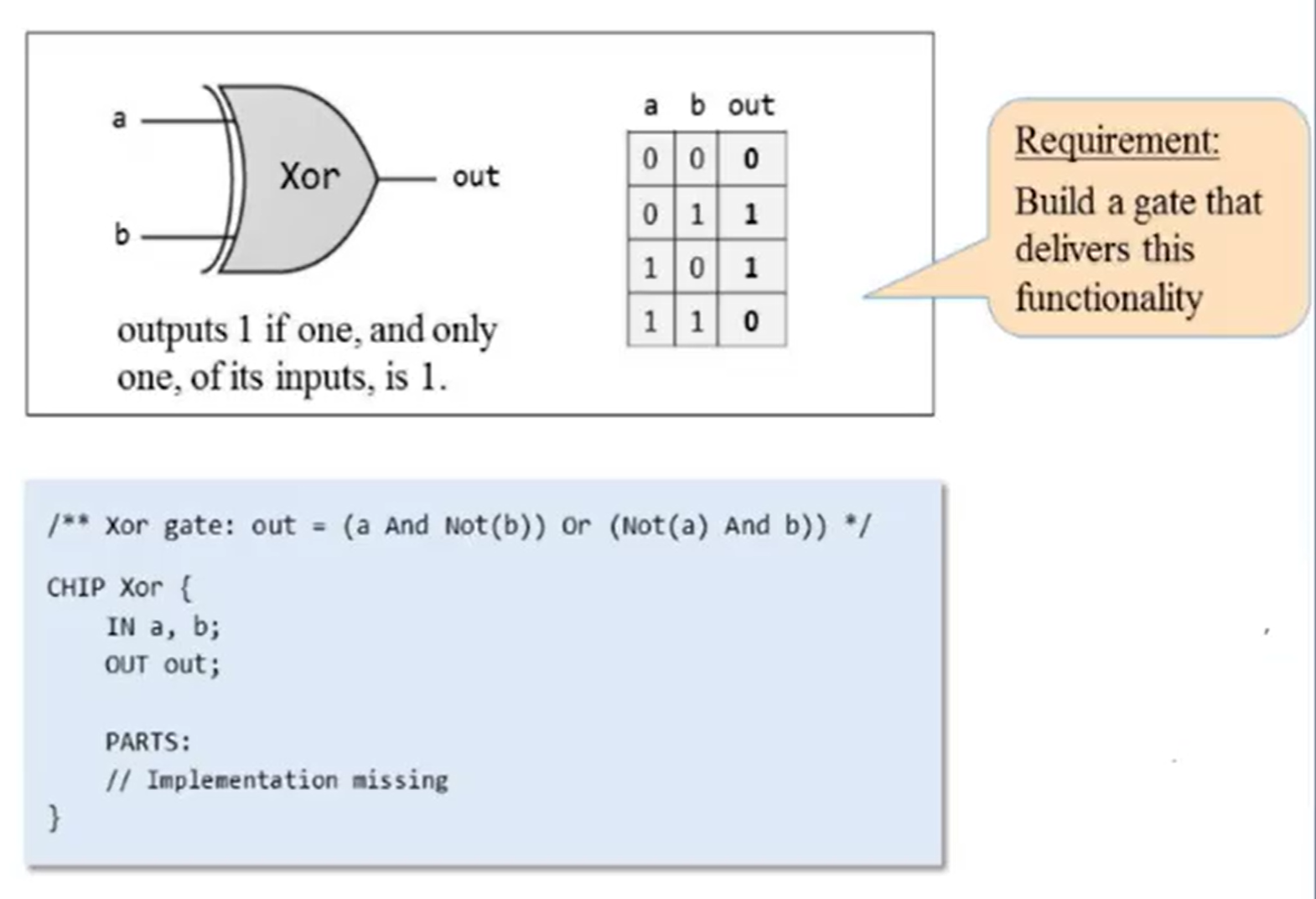
顺便说 所有这些芯片的名称及其输入和输出的名称通常都会提供给你。这不是你自己决定的事情。因此你只需用HDL语法写出来 它描述了这个芯片的实际设计方式的程序片段。



